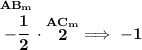check the picture below.
so... let's check those slopes then. Notice the triangle, the triangle "seem" to have a right-angle at the vertex A, namely, the slopes of AB and AC are perpendicular if that's true.
Now, when the product of two perpendicular slopes is -1.
so, let's check the slopes then.
![\bf \begin{array}{ccccccccc} &&x_1&&y_1&&x_2&&y_2\\ % (a,b) &A&(~{{ -1}} &,&{{ 3}}~) % (c,d) &B&(~{{ 1}} &,&{{ 2}}~) \end{array} \\\\\\ % slope = m slope = {{ m}}\implies \cfrac{\stackrel{rise}{{{ y_2}}-{{ y_1}}}}{\stackrel{run}{{{ x_2}}-{{ x_1}}}}\implies \cfrac{2-3}{1-(-1)}\implies \cfrac{2-3}{1+1}\implies \cfrac{-1}{2}\\\\ -------------------------------\\\\]()
![\bf \begin{array}{ccccccccc} &&x_1&&y_1&&x_2&&y_2\\ % (a,b) &A&(~{{ -1}} &,&{{ 3}}~) % (c,d) &C&(~{{ -3}} &,&{{ -1}}~) \end{array} \\\\\\ % slope = m slope = {{ m}}\implies \cfrac{\stackrel{rise}{{{ y_2}}-{{ y_1}}}}{\stackrel{run}{{{ x_2}}-{{ x_1}}}}\implies \cfrac{-1-3}{-3-(-1)}\implies \cfrac{-1-3}{-3+1} \\\\\\ \cfrac{-4}{-2}\implies \cfrac{2}{1}\implies 2\\\\ -------------------------------]()
![\bf \begin{array}{ccccccccc} &&x_1&&y_1&&x_2&&y_2\\ % (a,b) &C&(~{{ -3}} &,&{{ -1}}~) % (c,d) &B&(~{{ 1}} &,&{{ 2}}~) \end{array} \\\\\\ % slope = m slope = {{ m}}\implies \cfrac{\stackrel{rise}{{{ y_2}}-{{ y_1}}}}{\stackrel{run}{{{ x_2}}-{{ x_1}}}}\implies \cfrac{2-(-1)}{1-(-3)}\implies \cfrac{2+1}{1+3}\implies \cfrac{3}{4}]()
now, let's check the product of AB and AC,