Question

a bag of 10 marbles contains seven striped Marbles and 3 black marbles in the first event Mark draws a striped marble he does not replace it in the next three events Mark draws a striped 2 striped Marbles and one black marble he does not replace those marbles either what is the probability that he will select a black marble on the 5th event . Teach me how to solve it it's out of a1:10 b1:3 c2:7 d 2:3 I think its d

Answer 1

The probabability that he will obtain a black marble is as follows.

Using the first event, since there are 7 striped marbles and there's a total of 10 marbles, the probability must be as follows:

`P=(7)/(10)`

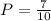
For the next three event, since there are no replacements, the denominators of each factor will be subtracted by 1. Thus, we have the following:

`P=(7)/(10)\cdot(\square)/(9)\cdot(\square)/(8)\cdot(\square)/(7)`

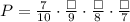
Since one striped marble is already taken in the first event, there must be 6 striped marbles left in the second event, and 5 on the third event. As for the fourth event, there are 3 black marbles based from the given. Thus, the probability up until the fourth event is as follows:

`P=(7)/(10)\cdot(6)/(9)\cdot(5)/(8)\cdot(3)/(7)`

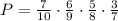
Finally, to find the probability that he will select a black marble on the fifth event, the fifth factor must have a denominator of 6 since 4 marbles were already taken out in the first 4 events. On the other hand, the numerator must be 2 since one black marble is taken out on the 4th event.

Thus, simplifying the probability, we have the following:

`P=(7)/(10)\cdot(6)/(9)\cdot(5)/(8)\cdot(3)/(7)\cdot(2)/(6)=(1)/(24)`

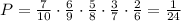
Therefore, the probability must be 1/24.