Question

The table shows the number of points scored by the Bearcats during their first five gamesPoints scored (X) 1. 2. 3. 4 5Number of games (f) 12 10 18. 4 6A.Create a probability distribution table. Show your work Round probability to the tenths place.B.What is the probability of the Bearcats scoring 4 points?C.What is the probability of the Bearcats scoring more than 1 point?D.What is the expected value of the number of points? Show your work.

Answer 1

a) From the table,

We need to create a probability distribution table.

Let x be the number of points scored.

The total number of games he played is 50.

So,

`\begin{gathered} P\mleft(x=1\mright)=(12)/(50) \\ =0.24 \\ P(x=2)=(10)/(50) \\ =0.2 \\ P(x=3)=(18)/(50) \\ =0.36 \\ P(x=4)=(4)/(50) \\ =0.08 \\ P(x=5)=(6)/(50) \\ =0.12 \end{gathered}`

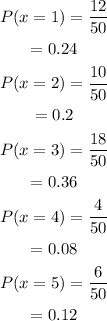
Hence, the probability distribution table is,

b)

To find the probability of the Bearcats scoring 4 points:

P(X=4)=0.08

Hence, the probability of the Bearcats scoring 4 points is 0.08.

c)

To find the probability of the Bearcats scoring more than 1 point:

`\begin{gathered} P\mleft(X>1\mright)=P\mleft(x=2\mright)+P\mleft(x=3\mright)+P\mleft(x=4\mright)+P\mleft(x=5\mright) \\ =0.20+0.36+0.08+0.12 \\ =0.76 \end{gathered}`

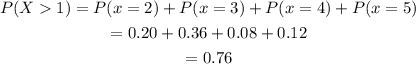
Hence, the probability of the Bearcats scoring more than 1 point is 0.76.

d) To find the expected value of the number of points:

`\begin{gathered} E(x)=\sum ^{}_{}xP(x) \\ =1(0.24)+2(0.20)+3(0.36)+4(0.08)+5(0.12) \\ =0.24+0.40+1.08+0.32+0.60_{} \\ =2.64 \end{gathered}`

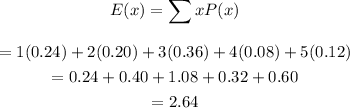
Hence, the expected value is 2.64.