a) From the table,
We need to create a probability distribution table.
Let x be the number of points scored.
The total number of games he played is 50.
So,
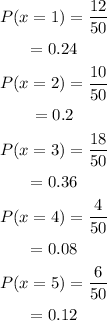
Hence, the probability distribution table is,
b)
To find the probability of the Bearcats scoring 4 points:
P(X=4)=0.08
Hence, the probability of the Bearcats scoring 4 points is 0.08.
c)
To find the probability of the Bearcats scoring more than 1 point:
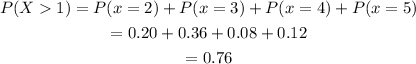
Hence, the probability of the Bearcats scoring more than 1 point is 0.76.
d) To find the expected value of the number of points:
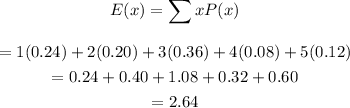
Hence, the expected value is 2.64.