Question

You can choose the same 3 answers for all of them

two real solutions

one real solution

no real solutions

Answer 1

Let
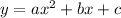
`y=ax^2+bx+c` be a quadratic equation; a is not equal to 0.


The discriminant of
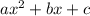
`ax^2+bx+c` is defined as
`D=b^2-4ac`.

The number of (real number) solutions of a quadratic equation is determined by the discriminant as follows:

If D>0, then the equation has 2 (different) solutions.

If D=0, the equation has 1 real solution.

If D<0, the equation has no real solutions.


Thus, we calculate the discriminants in each equation, and decide on the number of solutions accordingly:

i) a=-3, b=1, c=12; D=(-3)^2-4*1*12=9-48<0 (no real solutions).


ii) a=2, b=-6, c=5; D=2^2-4*(-6)*5=4+120>0 (2 real solutions).


iii) a=1, b=7, c=-11; D=1^2-4*7*(-11)=1+28*11>0 (2 real solutions).


iv) a=-1, b=-8, c=-12; D=(-1)^2-4(-8)(-12)=1-48*12<0 (no real solutions).


Answer: no solution, 2 solutions, 2 solutions, no solution.