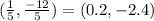Question

given the points M (-3,-4) and T (5,0), find the coordinates of the point Q on direct line segment MT that partitions MT in the ratio 2:3. Write the coordinates of the point Q in decimal form.

Answer 1

vector MT, or the change from x1 to x2 and y1 to y2 is expressed as

`(5 - ( - 3))i + (0 - ( - 4))j \\ = 8i + 4j`
no worries if you are unfamiliar with vector notation which is the the I and j there. it just shows that from point m to point t, x increases by 8 and y increases by 4. now find

`(2)/(3) 8 \: \: \: \: and \: \: \: \: (2)/(3) 4`
that is

`(16)/(3) and (8)/(3)`
add the 16/3 to the original value of x and 8/3 to the original value of y. the original value is point m.

now your point q should equal

`( (16)/(3) + ( - 3))x \: \: and \: \: ( (8)/(3) + ( - 4))y`

Answer 2

The coordinates of the point Q = (x,y) =(0.2,-2.4)

Explanation:

The section formula, (x,y) is the coordinate on line joining two points
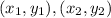`(x_1,y_1) , (x_2,y_2)` in the ratio of m is to n.

`x=(x_1* n+x_2* m)/(m+n)`

`y=(y_1* n+y_2* m)/(m+n)`

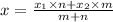
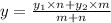
Given the points M (-3,-4) and T (5,0) , on this line joining these point there was another point Q which divides into ratio of 2:3.

`(x_1,y_1) , (x_2,y_2)=(-3,-4) , (5,0)`

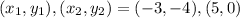
The coordinates of the point Q = (x,y)

m = 2 , n = 3

`x=(-3* 3+5* 2)/(2+3)`

`x=(1)/(5)=0.2`

`y=(-4* 3+0* 2)/(2+3)`

`y=(-12)/(5)=-2.4`

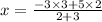
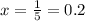
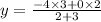
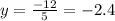
The coordinates of the point Q = (x,y) =
`((1)/(5),(-12)/(5))=(0.2,-2.4)`