Question

Complete the steps for deriving the quadratic formula using the following equation.

Answer 1

i think this is it. hope this helps

Answer 2

Having obtained:


`x^2+ (b)/(a)x+( (b)/(2a) )^2+ (c)/(a)-( (b)/(2a) )^2=0`

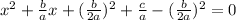
the next thing to do is collect the first three terms and write them as the square of a binomial, and also collect the last two terms, writing each of them with a denominator equal to 4a^2

We have:


`(x+(b)/(2a) )^2+( (4ac)/(4a^2)-(b^2)/(4a^2) )=0`.

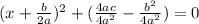
Then, we take
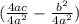
`( (4ac)/(4a^2)-(b^2)/(4a^2) )` to the right side and write these two terms as one:



`(x+(b)/(2a) )^2=(b^2-4ac)/(4a^2)`.


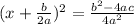
Next, we take the square root of both sides, which has been shown in the solution.


Next, we have to take b/2a to the right hand side as -(b/2a), and removing the square in the denominator of the right hand side expression:


`x=-(b)/(2a)\pm (√(b^2-4ac))/(2a)}`.



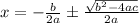
Answer: the steps to complete in the boxes are :



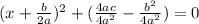
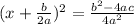
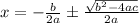
`(x+(b)/(2a) )^2+( (4ac)/(4a^2)-(b^2)/(4a^2) )=0`.


`(x+(b)/(2a) )^2=(b^2-4ac)/(4a^2)`.


`x=-(b)/(2a)\pm (√(b^2-4ac))/(2a)}`.