Answer:
only (1) , (2) and (3) can be written as sums or differences of two cubes
Explanation:
Given : Some expressions.
We have to choose the expressions that are sums or differences of two cubes.
The sums or differences of two cubes is written as
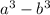 and
and
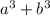
1)
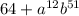
64 can written as
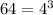 and
and
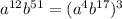
So,
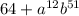 can be written as
can be written as
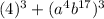
2)
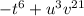
 can written as
can written as
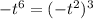 and
and

So,
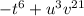 can be written as
can be written as

3)

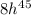 can written as
can written as
 and
and
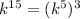
So,
 can be written as
can be written as
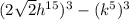
Thus, only (1) , (2) and (3) can be written as sums or differences of two cubes