Question

There are 8 people fishing at lake connor:4 with fishing licenses 4 do notAn inspector chooses 2 people at random. what is the probability that neither person has a license? write as fraction in the simplest form

Answer 1

The total number of sample space is

`n(S)=8`

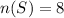
The number of people with fishing licenses is

`n(L)=4`

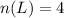
The number of people without a fishing license is

`n(W)=4`

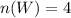
Step 1:

We will find the probability of picking the first person without a license, we will have

`Pr(W)=(n(W))/(n(S))`

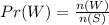
by substituting the values, we will have

`\begin{gathered} Pr(W)=(n(W))/(n(S)) \\ Pr(W_1)=(4)/(8)=(1)/(2) \end{gathered}`

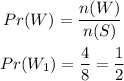
Step 2:

We will find the probability of picking the second person without a license,

Note:

There are 7 people left and 3 of them have a license left as we have picked one in step one

Hence,

The probability will be

`\begin{gathered} Pr(W_2)=(n(W_2))/(7) \\ Pr(W_2)=(3)/(7) \end{gathered}`

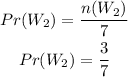
Step 3:

The probability of choosing two people without a license will be

`Pr(W_1W_2)=Pr(W_1)* Pr(W_2)`

By substituting the values, we will have

`\begin{gathered} Pr(W_1W_2)=Pr(W_1)* Pr(W_2) \\ Pr(W_1W_2)=(1)/(2)*(3)/(7)=(3)/(14) \end{gathered}`

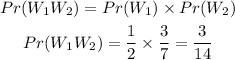
Hence,

The final answer = 3/14