Question

Did I do this right?

AD¯¯¯¯¯ , BD¯¯¯¯¯ , and CD¯¯¯¯¯ are angle bisectors of the vertex angles of △ABC . CF=8 meters and CD=17 meters.

What is DE ?

Answer 1

Yes I think so. AD¯¯¯¯¯ , BD¯¯¯¯¯ , and CD¯¯¯¯¯ are angle bisectors of the vertex angles of △ABC . CF=8 meters and CD=17 meters.
What is DE ? The answer is 15m.

Answer 2

Answer : The value of side DE is, 15 m

Step-by-step explanation :

First we have to determine the side DF.

Using Pythagoras theorem in ΔDFC :

`(Hypotenuse)^2=(Perpendicular)^2+(Base)^2`

`(CD)^2=(DF)^2+(CF)^2`

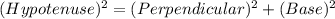
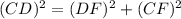
Given:

Side CD = 8 m

Side CF = 17 m

Now put all the values in the above expression, we get the value of side DF.

`(8)^2=(DF)^2+(17)^2`

`DF=√((17)^2-(8)^2)`

`DF=15m`

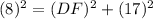
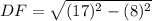
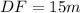
Now we have to determine the value of side DE.

Side DE = Side DF = 15 m (By congruent triangle DFB and DEB)

The ΔDFB and ΔDEB are congruent triangles.

Proof:

Side DB = Side DB (common side)

∠DBE = ∠DBF (BD is angle bisector, so these angle are always equal)

∠E = ∠F (equal to 90°)

ΔDFB ≅ ΔDEB (By SAS congruency)

So, Side DE = Side DF

Hence, the value of side DE is, 15 m