Question

Which of the following describes the domain of y = tan x, where n is any integer? A.x≠2nπ B. x≠π/2+nπ C. x≠nπ D.x≠nπ/2

Answer 1

y=tanx=sinx/cosx we cant divide by 0 so

cosx=0 would be a problm
cosx=0 when x=pi/2,3pi/2,...(2n+1)pi/2
(2n+1)pi/2=(2npi+pi)/2=2npi/2+pi/2=npi+pi/2
so its B

Answer 2

The correct answer is: Option (B)
`(\pi)/(2) + n\pi`

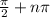
Step-by-step explanation:

Given function:

`y = tan(x)`

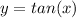
We know that,

`tan(x) = (sin(x))/(cos(x))`

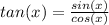
To find the domain, put the "denominator" equal to zero, as follows:

`cos(x) = 0`

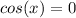
Now ask yourself the following question to find domain: For what values of x, will
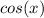`cos(x)` be equal to 0? Well, for
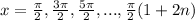`x = (\pi )/(2), (3\pi)/(2),(5\pi)/(2),..., (\pi)/(2)(1+2n)` where n = any integer.

Therefore, the domain of y = tan(x) is:

`(\pi)/(2)(1+2n)\\(\pi)/(2) + (2n\pi)/(2)\\`

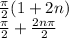
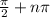`(\pi)/(2) + n\pi` (Option B)