Question

FIGURE 2 shows a 1.5 kg block is hung by a light string which is wound around a smooth pulley of radius 20 cm. The moment of inertia of the pulley is 2 kg m².(i) When the mass is released from rest, calculate the angular velocity and number of revolutions of the pulley at t = 4.2 s.

Answer 1

At t = 4.2 s

Angular velocity: 6. 17 rad /s

The number of revolutions: 2.06

Step-by-step explanation:

First, we consider all the forces acting on the pulley.

There is only one force acting on the pulley, and that is due to the 1.5 kg mass attached to it.

Therefore, the torque on the pulley is

`\tau=Fd=mg\cdot R`

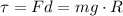
where m is the mass of the block, g is the acceleration due to gravity, and R is the radius of the pulley.

Now we also know that the torque is related to angular acceleration α by

`\tau=I\alpha`

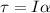
therefore, equating this to the above equation gives

`mg\cdot R=I\alpha`

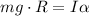
solving for alpha gives

`\alpha=(mgR)/(I)`

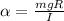
Now putting in m = 1.5 kg, g = 9.8 m/s^2, R = 20 cm = 0.20 m, and I = 2 kg m^2 gives

`\alpha=(1.5\cdot9.8\cdot0.20)/(2)`
`\boxed{\alpha=1.47s^(-2)}`

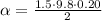
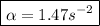
Now that we have the value of the angular acceleration in hand, we can use the kinematics equations for the rotational motion to find the angular velocity and the number of revolutions at t = 4.2 s.

The first kinematic equation we use is

`\theta=\theta_0+\omega_0t+(1)/(2)\alpha t^2`

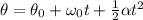
since the pulley starts from rest ω0 = 0 and theta = 0; therefore, we have

`\theta=(1)/(2)\alpha t^2`

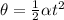
Therefore, ar t = 4.2 s, the above gives

`\theta=(1)/(2)(1.47)(4.2)^2`

`\boxed{\theta=12.97}`

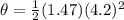
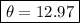
So how many revolutions is this?

To find out we just divide by 2 pi:

`\#\text{rev}=(\theta)/(2\pi)=(12.97)/(2\pi)`
`\boxed{\#\text{rev}=2.06}`

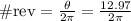
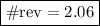
Or about 2 revolutions.

Now to find the angular velocity at t = 4.2 s, we use another rotational kinematics equation:

`\omega^2=w^2_0+2\alpha(\Delta\theta)_{}`

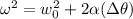
Since the pulley starts from rest, ω0 = 0. The change in angle Δθ we calculated above is 12.97. The value of alpha we already know to be 1.47; therefore, the above becomes:

`\omega^2=0+2(1.47)(12.97)`
`w^2=38.12`
`\boxed{\omega=6.17.}`

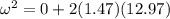
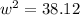
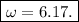
Hence, the angular velocity at t = 4.2 w is 6. 17 rad / s

To summerise:

at t = 4.2 s

Angular velocity: 6. 17 rad /s

The number of revolutions: 2.06