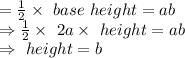Answer: 1. Coordinates of N=(a,b).
2. Area of ΔKNM=ab.
3. Base of ΔMNL= 2a and height =b.
Step-by-step explanation
1. Given: ΔKML in which N is the midpoint of L(2a,0) and and K(0,2b)
By mid point theorem the coordinates of N =
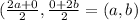
2. Given: In ΔKNM , base MK=2b and height=a then
Area of ΔKNM=
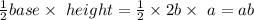
3.Given: Area of ΔMNL =ab
base of ΔMNL=2a ,across x axis.
Now ,
Arera of ΔMNL