Question

What is the completely factored form of x4 + 8x2 – 9?

A(x + 1)(x – 1)(x + 3)(x + 3)
B(x + 1)(x - 1)(x2 + 9)
C(x2 – 1)(x + 3)(x – 3)
D(x + 1)(x + 1)(x + 3)(x + 3)

Answer 1

The answer is B:

`{x}^(4) + 8 {x}^(2) - 9`

`= ( {x}^(2) + 9)( {x}^(2) - 1)`

`= (x + 1)(x - 1)( {x}^(2) + 9)`
Hope this helped

Answer 2

ANSWER

The correct answer is B


Step-by-step explanation

We want to factor completely,

`{x}^(4) + 8 {x}^(2) - 9`


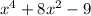
We can rewrite the above expression in the form.



`{( {x}^(2)) }^(2) + 8( {x}^(2) ) - 9`


We can think of this expression as a quadratic trinomial in

`{x}^(2)`


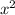
We need to split the middle term with factors of -9 that adds up to 8.




`{( {x}^(2)) }^(2) - {x}^(2) + 9{x}^(2) - 9`


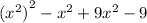
We factorize to obtain,


`{x}^(2) ( {x}^(2) - 1) + 9( {x}^(2) - 1)`



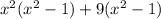
We factor further to obtain,


`({x}^(2) - 1)( {x}^(2) + 9)`


We apply difference of two squares on the leftmost factor to obtain,



`(x - 1)(x + 1)( {x}^(2) + 9)`