Question

What is the interest earned on $20,000 for five years, at an interest rate of 3 3/5 % compounded continuously?

Answer 1

`\bf ~~~~~~ \textit{Continuously Compounding Interest Earned Amount}\\\\ A=Pe^(rt)\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\to& \$20000\\ r=rate\to 3(3)/(5)\%\to (3(3)/(5))/(100)\to (18)/(500)\to &0.036 \\ t=years\to &5 \end{cases} \\\\\\ A=20000e^(0.036\cdot 5)\implies A=20000e^(0.18)\implies A\approx 23944.3487262`

Answer 2

23,944.35

Explanation:

Initial amount (principal) is 20,000

rate of interest is 3 3/5=
`3 (3)/(5) =(18)/(5)=3.6`

Divide by 100 to remove %, so its 0.036

compounding continuously formula is

`A=Pe^(rt)`

Where P is the initial amount

'r' is the rate of interest=0.036

t is the number of years=5

Plug in all the values in the formula

`A=Pe^(rt)`

`A=20000e^(0.036 \cdot 5)`

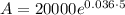
A= 23944.34726

A= 23,944.35