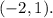Question

What are the coordinates of the circumcenter of a triangle with vertices A(−3, 3) , B(−1, 3) , and C(−1, −1) ?

Enter your answer in the box. ( , )

Answer 1

The answer to this is (-2, 1).

Answer 2

ANSWER

The circumcenter of ∆ABC has coordinates

`(-2,1)`

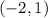
Step-by-step explanation

The circumcenter is the point of intersection of the perpendicular bisectors of any two sides of triangle ABC.

Considering side AB with coordinates (-3,3) and (-1,3) respectively, we can see that this is a horizontal line. The perpendicular bisector of this line is a vertical line that has equation x equals the x-coordinate of the midpoint of AB.

Midpoint of AB has coordinates


`( ( - 3 + - 1)/(2) , (3 + 3)/(2) )`

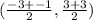
This gives


`( ( - 4)/(2) , (6)/(2) )`


`( - 2, 3)`

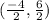
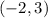
The equation of the perpendicular bisector is

`x = - 2`

Similarly, the coordinates of B(-1,3) and C(-1,-1) tells us that, line BC is a horizontal line since the x-values are constant. Therefore the perpendicular bisector is a horizontal line that has equation , y equals the y-value of the midpoint of BC.

The midpoint of BC has coordinates,


`( ( - 1 + - 1)/(2) , (3 + - 1)/(2) )`

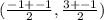
This implies that,


`( ( - 2)/(2) , (2)/(2) )`

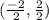
This gives,


`( - 1 , 1)`

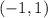
The equation of the perpendicular bisector is

`y = 1`

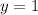
These two bisectors will meet at,


`(-2,1)`

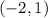
Therefore the circumcenter is

`(-2,1).`