Question

I don't need you to work it out, just theorem(s) i need to reach the answer :)

Answer 1

Not sure why such an old question is showing up on my feed...

Anyway, let
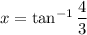
`x=\tan^(-1)\frac43` and
`y=\sin^(-1)\frac35`. Then we want to find the exact value of
`\cos(x-y)`.

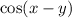
Use the angle difference identity:


`\cos(x-y)=\cos x\cos y+\sin x\sin y`

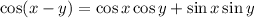
and right away we find
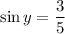
`\sin y=\frac35`. By the Pythagorean theorem, we also find
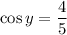
`\cos y=\frac45`. (Actually, this could potentially be negative, but let's assume all angles are in the first quadrant for convenience.)

Meanwhile, if
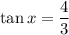
`\tan x=\frac43`, then (by Pythagorean theorem)
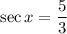
`\sec x=\frac53`, so
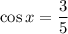
`\cos x=\frac35`. And from this,
`\sin x=\frac45`.

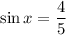
So,


`\cos\left(\tan^(-1)\frac43-\sin^(-1)\frac35\right)=\frac35\cdot\frac45+\frac45\cdot\frac35=(24)/(25)`