Question

A particle’s position along the x-axis is described byx(t) = A t + B t2,where t is in seconds, x is in meters, and the constants A and B are given below.Randomized VariablesA = -3.15 m/sB = 2.4 m/s21 what is the position of the particle when the velocity is zero.

Answer 1

Given data:

Position of the particle along the x-axis;

`x(t)=At+Bt^2`

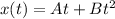
Here, A and B are constants with A=-3.15 m/s and B=2.4 m/s².

Therefore,

`x(t)=-3.15t+2.4t^2`

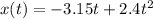
The velocity of the particle is given as,

`v(t)=(dx(t))/(dt)`

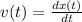
Substituting x(t),

`\begin{gathered} v(t)=(d)/(dt)(-3.15t+2.4t^2) \\ =(d)/(dt)(-3.15t)+(d)/(dt)(2.4t^2) \\ =-3.15+2*2.4t \\ =-3.15+4.8t \end{gathered}`

The time when the velocity will be zero is calculated by substituting v(t)=0 in the above expresion,

`\begin{gathered} 0=-3.15+4.8t \\ 4.8t=3.15 \\ t=(3.15)/(4.8) \\ \approx0.66\text{ s} \end{gathered}`

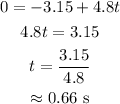
Therefore, the position of the particle when the velocity is zero is calculated by substituting t=0.66 s in the equation for the position of the particle,

`\begin{gathered} x(0.66\text{ s})=-3.15*0.66+2.4*(0.66)^2 \\ \approx-1.03\text{ m} \end{gathered}`

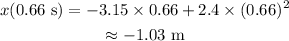
Therefore, the position of the particle when the velocity is zero is -1.03 m (1.03 m to the left of its initial position).