Question

jose is choosing a 3-letter password from the letters a,b,c,d. the password cannot have the same letter repeated in it. how many passwords are possible

Answer 1

Alright, so we are dealing with permutations. Permutations are the number of combinations in a specific order possible for the set.

There's 4 letters, each one can be paired with 3 other letters, but those letters could be in different orders. To figure out how many variations of each combination there are (aka the number of permutations) use this formula:


`_(n)P_(r)= (n!)/((n-r)!)`


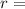
`r=` number of elements in the subset


`n=` number of elements in the set


`P=` permutations of the set

There are only 3 elements in the subset because there is 1 that will not be repeated in each set, and there are 4 elements in the set.

Here's the math:


`_(n)P_(r)= (n!)/((n-r)!)`


`_(4)P_(3)= (4!)/((4-3)!)`


`_(4)P_(3)= (4!)/((1)!)`


`_(4)P_(3)= (4(3)(2)(1))/(1)`


`_(4)P_(3)=24`

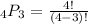
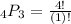
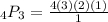
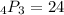
There are 24 permutations. I can prove this by showing you the model:

ABCD, ABDC, ACBD, ACDB, ADBC, ADCB are the 6 arrangements possible of the set starting with the letter A. Because there are 4 letters, the total amount of permutations without repeated letters is 4 (letters) times 6 (possible arrangements), which equals 24.

Hope this helps!

Answer: 24 passwords are possible