Graph y < x^2 + 2. Click on the graph until the correct one appears.

Question

asked Jul 28, 2018 103k views

2 Answers

Neildo · Answer 1 · 2018-08-03T18:22:17+0000

Answer:

The graph of given inequality is attached below.

Explanation:

The given inequality is

y<x^2+2

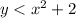
The related equation of the of the given inequality is

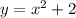y=x^2+2 .... (1)

The related curve is dotted because the sign of inequality is <. The points on the curve are not included in the solution set.

It is a quadratic equation. So, the graph of related equation is a parabola.

The vertex form of a parabola is

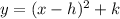y=(x-h)^2+k .... (2)

From (1) and (2), we get

h=0,k=2

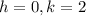
The vertex of the parabola is at (0,2).

At x=1,

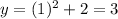
y=(1)^2+2=3

At x=-1,

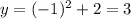
y=(-1)^2+2=3

It means the graph if passing through (1,3) and (-1,3).

Check the inequality by (0,0),

(0)<(0)^2+2

0<2

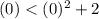
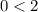
This statement is true, it means (0,0) is in the shaded region.

The graph of given inequality is attached below.