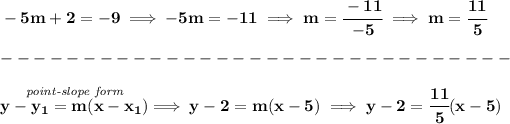so we know it passes through 5,2, and has the same y-intercept as y = 3x -9.... hmmmm
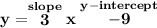
.
so this one has a y-intercept at -9, therefore this line must have the same y-intercept... let's say it has a slope of "m".
![\bf \begin{array}{ccccccccc} &&x_1&&y_1\\ % (a,b) &&(~{{ 5}} &,&{{ 2}}~) \end{array} \\\\\\ % slope = m slope = {{ m}} \\\\\\ % point-slope intercept \stackrel{\textit{point-slope form}}{y-{{ y_1}}={{ m}}(x-{{ x_1}})}\implies y-2=m(x-5)\implies y-2=mx-5m \\\\\\ y=mx-5m+2\implies y=\stackrel{slope}{m}x\stackrel{y-intercept}{-5m+2}]()
so, this one has a y-intercept of "-5m+2", which we know is the same as the other equation's, therefore
-5m+2 = -9.