Question

Which ordered pairs lie on the graph of the exponential function f(x)=2^(x+4)−8?

Select each correct answer.



​ (2,  56) ​

​​ (−2,−4)(−2,−4)

​ (8,  0) ​ ​

​​ (24,  1) ​

Answer 1

(24,1)

Explanation:

Answer 2

Given the function


`f(x)=2^((x+4))-8`

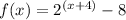
Consider the point (2, 56) i.e. when x = 2


`f(x)=2^(2+4)-8 \\ \\ =2^6-8=64-8 \\ \\ =56`

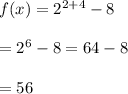
Therefore, point (2, 56) lie on the graph of the given exponential function.

Consider the point (-2, -4) i.e. when x = -2


`f(x)=2^(-2+4)-8 \\ \\ =2^2-8=4-8 \\ \\ =-4`

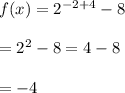
Therefore, point (-2, -4) lie on the graph of the given exponential function.

Consider the point (8, 0) i.e. when x = 8


`f(x)=2^(8+4)-8 \\ \\ =2^(12)-8=4,096-8 \\ \\ =4,088`

Therefore, point (8, 0) does not lie on the graph of the given exponential function.

Consider the point (24, 1) i.e. when x = 24


`f(x)=2^(24+4)-8 \\ \\ =2^(28)-8=268,435,456-8 \\ \\ =-268,435,448`

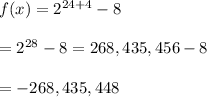
Therefore, point (24, 1) does not lie on the graph of the given exponential function.