Given the roots of the quadratic equation to be
-3 and 5
This implies that x = -3 or x = 5
Equate the two roots to 0
Therefore, x + 3 = 0 or x - 5 = 0
(x + 3) (x - 5) = 0
Open the parentheses
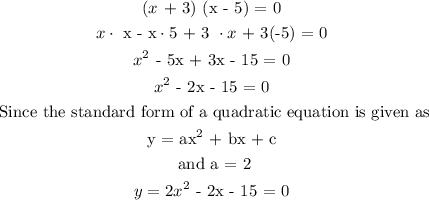
y = 2x^2 + (-2)x + (-15)
The first blank is 2
The second blank is -2
The third blank is -15