Question

A student decides to have fun by throwing his physics book through the window of the laboratory located 25m above the ground, with an initial speed of 20 m / s upwards. Gravity acceleration : 10m / s After how long will the book reach its maximum height? What maximum height will the book reach? The time at which the book will have reached a height of 30m ?The speed of the book when its height is 30m ?The speed and height of the book at t = 4.5s ?

Answer 1

We are given an object is thrown from a height of 25 meters with a speed of 20 m/s. We are asked to determine the time for the maximum height. To do that we will use the following formula:

`y=y_0+v_0t-(1)/(2)gt^2`

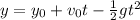
Where:

`\begin{gathered} y_0=\text{ initial height} \\ v_0=\text{ initial velocity} \\ t=\text{ time} \\ g=\text{ acceleration of gravity} \\ y=\text{ height at time t} \end{gathered}`

Now, this formula is a parabola of the form:

`y=c+bt+at^2`

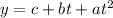
The time for the maximum height is determined at the vertex of the parabola. The formula for the t-coordinate of the vertex is:

`t=-(b)/(2a)`

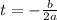
Substituting the values:

`t=-(v_0)/(2(-(1)/(2)g))`

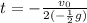
Now we simplify and we get:

`t=(v_0)/(g)`

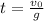
Now we substitute the values and we get:

`t=(20(m)/(s))/(10(m)/(s^2))`

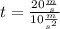
Solving the operations we get:

`t=2s`

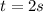
Therefore the maximum height is reached after 2 seconds.

Now we are asked to determine what is the value of the maximum height. To do that we go back to the formula for the height:

`y=y_0+v_0t-(1)/(2)gt^2`

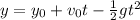
Now we substitute the known values of initial height, initial speed and acceleration of gravity, we get:

`y=25m+20(m)/(s)t-(1)/(2)(10(m)/(s^2))t^2`

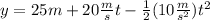
Simplifying we get:

`y=25m+20(m)/(s)t+5(m)/(s^2)t^2`

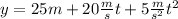
Now, since we want the maximum height we replace the value of the time for the maximum height that we determined previously, that is t = 2s, we get:

`y=25m+20(m)/(s)(2s)-5(m)/(s^2)(2s)^2`

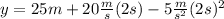
Solving the operations we get:

`y=45m`

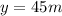
Therefore, the maximum height is 45 meters.

Now we are asked to determine the time at which the book will have reached a height of 30 meters. We will replace the value of y = 30 in the equation for height, we get:

`y=25m+20(m)/(s)t-5(m)/(s^2)t^2`

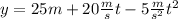
Substituting y = 30, we get:

`25+20t-5t^2=30`

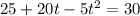
From this point on we will not write the units in order to make the notation less dense.

Now we get a quadratic equation. We will subtract 30 from both sides:

`\begin{gathered} 25-30+20t-5t^2=30-30 \\ -5+20t-5t^2=0 \end{gathered}`

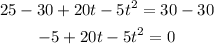
Now we multiply both sides by -1:

`5t^2-20t+5=0`

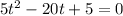
Dividing both sides by 5 we get:

`t^2-4t+1=0`

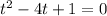
Now we use the quadratic formula to solve the equation:

`t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Now we substitute the values according to the values of a, b, and c that we defined for a quadratic (parabola) equation. We get:

`t=\frac{-(-4)\pm\sqrt[]{(-4)^2-4(1)(1)}}{2(1)}`

Solving the operations we get:

`t=\frac{4\pm\sqrt[]{12}}{2}`

Now we factor the term inside the radical:

`t=\frac{4\pm\sqrt[]{4*3}}{2}`

Distributing the radical:

`t=\frac{4\pm\sqrt[]{4}\sqrt[]{3}}{2}`

Solving the operations:

`t=\frac{4\pm2\sqrt[]{3}}{2}`

Now we distribute the denominator:

`t=(4)/(2)\pm\frac{2\sqrt[]{3}}{2}`

Simplifying:

`t=2\pm\sqrt[]{3}`

Therefore, there are two points in time where the object reaches a height of 30 meters, these are:

`t=2+\sqrt[]{3}=3.73`

And:

`t=2-\sqrt[]{3}=0.26`

Each of the values is in seconds.

Now we are asked to determine the speed when the height is 30 meters. To do that we will use the following formula for the speed:

`v=v_0-gt`

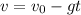
Now we substitute the known values:

`v=20-10t`

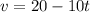
Now we substitute the first value of time:

`v=20-10(3.73)`

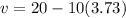
Solving the operations:

`v=-17.3`

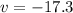
We get -17.3 m/s. Now we substitute the second value of time:

`v=20-10(0.26)`

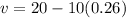
Now we solve the operations:

`v=17.4`

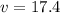
The velocity is 17.4 m/s. We get approximately the same value but with the sign inverted. This is because at the same height we will have a velocity upwards (positive) and another velocity downwards (negative) but with the same magnitude.

Now we are asked to determine the speed of the object when the time is t = 4.5s. We will apply the formula for velocity:

`v_{}=20-10t`

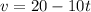
Substituting t = 4.5 we get:

`\begin{gathered} v=20-10(4.5) \\ v=-25 \end{gathered}`

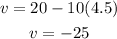
The velocity is -25 m/s.

To determine the height we use the formula for the height, we get:

`y=25+20t-5t^2`

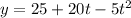
Substituting the value of "t":

`y=25+20(4.5)-5(4.5)^2`

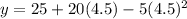
Solving the operations we get:

`y=13.75`

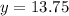
Therefore, the height is 13.75 meters.