Question

A quarterback throws a football with a velocity of 41 mph and a direction of 168°. The wind on the field is 11 mph with a direction of 339°. What are the true speed and direction of the football? Round the speed to the thousandths place and the direction to the nearest degree.

Answer 1

Given:

A quarterback throws a football with a velocity of 41 mph and a direction of 168°.

The wind on the field is 11 mph with a direction of 339°

So, there are 2 vectors:

`\begin{gathered} v=41\angle168\degree \\ w=11\angle339\degree \end{gathered}`

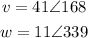
We will find the resultant speed as the sum of the vectors v and w

`\begin{gathered} R=v+w=41\angle168\degree+11\angle339\degree \\ \end{gathered}`

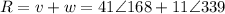
To find the sum of the vectors, convert from the polar form to the rectangular form:

`\begin{gathered} R=(41\cos 168+11\cos 339)i+(41\sin 168+11\sin 339)j \\ R=-29.835i+4.582j \end{gathered}`

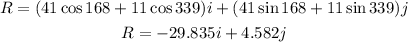
Now, we will convert from the rectangular form to the polar form to express the resultant as magnitude and angle:

`\begin{gathered} |R|=\sqrt[]{(-29.835)^2+(4.582)^2}=30.185 \\ \theta=\tan ^(-1)(4.582)/(-29.835)\approx171.268 \end{gathered}`

So, the answer will be the second option: 30.185, 171°