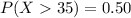Given the Mean:
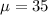
And the Standard Deviation:
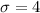
You need to find:
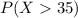
You can find the z-statistics using this formula:
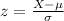
In this case, you need to set up that:
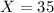
Then, substituting values and evaluating, you get:
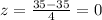
Therefore, you need to find:
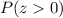
Using the Normal Distribution Table for that z-statistic, you get:
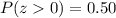
Hence, the answer is: