Question

Two cars are headed in the same direction on the HWY. The trailing car is moving at14.5 m/s and has a mass of 1,381 kg. The lead car is moving at 13.4 m/s and has a massof 1,381 kg. The trailing car runs into the lead car and bumps it. Afterwards, the trailingcar has a velocity of 13.4 m/s.To determine if the collision is elastic, calculateAKE=KE - KE

Answer 1

The initial momentum of the system is,

`p_i=m_1u_1+m_2u_2`

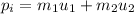
The final momentum of the system is,

`p_f=m_1v_1+m_2v_2`

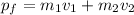
According to conservation of momentum,

`p_i=p_f`

Plug in the known expressions,

`\begin{gathered} m_1u_1+m_2u_2=m_1v_1+m_2v_2 \\ m_2v_2=m_1u_1+m_2u_2-m_1v_1 \\ v_2=(m_1u_1+m_2u_2-m_1v_1)/(m_2) \end{gathered}`

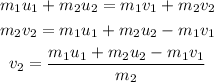
Substitute the known values,

`\begin{gathered} v_2=\frac{(1381\text{ kg)(14.5 m/s)+(1381 kg)(13.4 m/s)-}(1381\text{ kg)(13.4 m/s)}}{1381\text{ kg}} \\ =\frac{(1381\text{ kg)(14.5 m/s)}}{1381\text{ kg}} \\ =14.5\text{ m/s} \end{gathered}`

The initial kinetic energy of the system is,

`K=(1)/(2)m_1u^2_1+(1)/(2)m_2u^2_2`

The final kinetic energy of the system is,

`K^(\prime)=(1)/(2)m_1v^2_1+(1)/(2)m_2v^2_2`

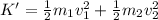
The change in kinetic energy of the system is,

`\Delta K=K^(\prime)-K`

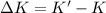
Plug in the known expressions,

`\begin{gathered} \Delta K=(1)/(2)m_2v^2_2+(1)/(2)m_1v^2_1-((1)/(2)m_2u^2_2+(1)/(2)m_1u^2_1) \\ =(1)/(2)m_2(v^2_2-u^2_2)+(1)/(2)m_1(v^2_1-u^2_1) \end{gathered}`

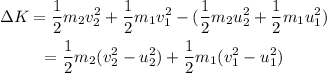
Substitute the known values,

`\begin{gathered} \Delta K=(1)/(2)(1381kg)((14.5m/s)^2-(13.4m/s)^2)- \\ (1)/(2)(1381kg)((13.4m/s)^2-(14.5m/s)^2) \\ =(690.5\text{ kg)(}210.25m^2s^(-2)-179.56\text{ }m^2s^(-2))-(690.5\text{ kg)(}179.56\text{ }m^2s^(-2)-210.25\text{ }m^2s^(-2)) \\ =(690.5\text{ kg)(}30.69\text{ }m^2s^(-2))(\frac{1\text{ J}}{1\text{ kg}m^2s^(-2)})-(690.5\text{ kg)(-30.69 }m^2s^(-2)) \\ =21191.4\text{ J+21191.4 J} \\ =42382.8\text{ J} \end{gathered}`

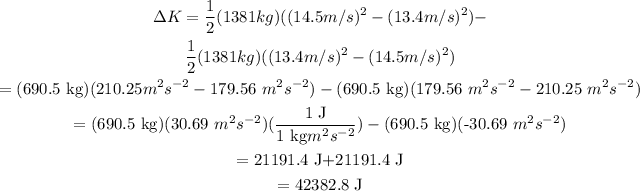
Therefore, the change in kinetic energy of the system is 42382.8 J.