Question

A carpenter wants to place carpet in a bedroom. The area of the rectangular floor is represented by the expression 12x^3 + 18x^2 - 24x If the length of the floor is 6x, what is the width of the floor?

Answer 1

divide the expression for the area by the length 6x ( width = area/length)

this gives the width :-

= 2x^2 + 3x - 4 Answer

Answer 2

The width of the floor is
`2x^2+3x-4`.

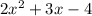Explanation:

It is given that the area of the rectangular floor is represented by the expression

`12x^3+18x^2-24x`

The area of a rectangle is

`A=length* width`

`(A)/(length)=width`

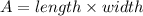
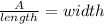
It is giver that the length of the floor is 6x. So, the width of the floor is

`width=(12x^3+18x^2-24x)/(6x)`

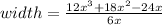
It can be written as

`width=(12x^3)/(6x)+(18x^2)/(6x)-(24x)/(6x)`

`width=2x^2+3x-4`

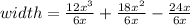
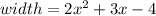
Therefore the width of the floor is
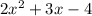`2x^2+3x-4`.