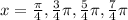Question

Use trigonometric identities and algebraic methods, as necessary, to solve the following trigonometric equation. Please identify all possible solutions by including allanswers in [O, 2.) and indicating the remaining answers by using n to represent any integer. Round your answer to four decimal places, if necessary. If there is nosolution, indicate "No Solution."sec(x) + 4 = 6

Answer 1

We can use the trig identity:

`1+\tan ^2\alpha=\sec ^2\alpha`

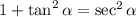
Then we rewrite and solve for tan:

`\begin{gathered} 1+\tan ^2x=6-4 \\ \tan ^2x=2-1 \\ \tan ^2x=1 \end{gathered}`

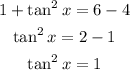
Now we can apply square root on both sides:

`|\tan x|=1`

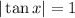
(We use the absolute value because tan^2 only can give possitive results)

Finally, we can use the identity:

`\tan \alpha=(\sin \alpha)/(\cos \alpha)`

Thus:

`|(\sin x)/(\cos x)|=1`

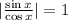
We are looking for values of sine and cosine that are equal in absolute value. We know that this happens for the first time in pi/4 and happens every pi/2 from there.

Thus, the solutions are:

`x=(\pi)/(4),(3)/(4)\pi,(5)/(4)\pi,(7)/(4)\pi`