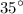Answer:
{35}^{\circ}
Explanation:
GIven: In Δ
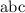 , the measure of angle
, the measure of angle
 is fifteen less than twice the measure of
is fifteen less than twice the measure of
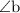 . the measure of angle
. the measure of angle
 equals the sum of the measures of angle
equals the sum of the measures of angle
 and angle
and angle
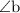 .
.
To Find: determine the measure of angle
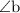 .
.
Solution:
In Δ
 ,
,
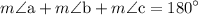
also,
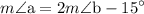
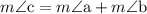
putting value of
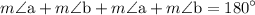


putting value of

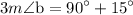
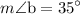
Therefore
 is
is