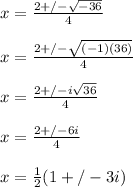The Quadratic Formula:
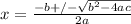
The discriminant is the part of the quadratic formula that's under the square root. (b² - 4ac)
The discriminant tells you how many solutions and what type of solutions (real, non-real) there are.
When the discriminant is 0; there is only one real solution.
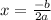
When the discriminant is a +positive number, There are two real solutions. One for the +√(discriminant) and one for -√(discriminant) in the +/- part of the quadratic formula.
When the discriminant is negative. There are two non-real solutions using the imaginary number i = √(-1)
For your problem: 2x² - 2x + 5
a = 2
b = -2
c = 5
plug these numbers into the quadratic formula:
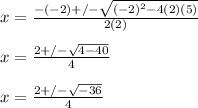
Here you can see the discriminant = -36 is a negative number. There will be 2 non-real solutions.