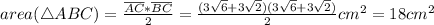Answer:
The area of △ABC is
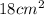
Explanation:
We are given a right triangle △ABC, with m∠C = 90°, m∠A = 75°, and AB = 12 cm. If we graph all the triangle data, we can see that we have the length of the hypotenuse, and one of the angles.
Using the trigonometric functions sine, cosine and tangent (Remember SOH CAH TOA), we can calculate the triangle legs, in the following form:
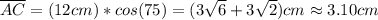
for the leg
 , and
, and
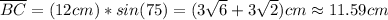
for the leg
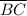 .
.
Finally, to know the area, we just use the area of a triangle formula: