How do the areas of the parallelogram compare?

Question

asked Aug 23, 2018 136k views

2 Answers

Asim Mahar · Answer 1 · 2018-08-29T17:18:31+0000

Solution:

Area of Parallelogram = Base × Height

Opposite Sides of Parallelogram are equal.

⇒ Area of Parallelogram 1 ,

Since it is a Rectangle , because Adjacent sides have angle between their legs has measure equal to 90°.

Product of slopes

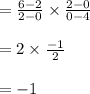
$=(6-2)/(2-0) * (2-0)/(0-4)\\\\=2 * (-1)/(2)\\\\= -1$

Area of Rectangle=Length × Breadth

$=√((2-0)^2+(6-2)^2)* √((0-4)^2 * (2-0)^2)}\\\\=√(20)* √(20)\\\\=20$ Square units

⇒Area of Parallelogram 2,

$\text{Base}=√((2-0)^2+(-8+2)^2)\\\\=√(40)\\\\=2√(5)\\\\Height=√([2-(-0.4)]^2+[0-(-1)]^2)=√(5.76+1)\\\\=√(6.76)\\\\=2.6$

Height =2.6 units

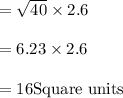$=√(40) * 2.6\\\\=6.23 * 2.6\\\\=16 \text{Square units}$ Approx

⇒≡ Difference in Area

=Area of Parallelogram 1 - Area of Parallelogram 2

=20 -16

=4 Square units

Option A:

Area of Parallelogram 1 is 4 unit greater than area of Parallelogram 2.