Question

x=0,0.5,1.5,2,2.5,3,3.5y=96,95,88,85,84,76,75Find the estimated value of y when x= 1.5.Round the answer to 3 decimal places.

Answer 1

EXPLANATION

Given that we have the data set, we can apply the following representation:

x=0,0.5,1.5,2,2.5,3,3.5

y=96,95,88,85,84,76,75

Building the following table:

Then we have:

`\bar{x}=(13)/(7)=1.857`
`\bar{y}=(599)/(7)=85.57`

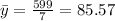
Now,

`b_(yx)=\frac{\sum^{}_{}xy-\frac{\sum^{}_{}x\sum^{}_{}y}{n}}{\sum^{}_{}x^2-(\frac{(\sum^{}_{}x)^2}{n})}`

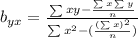
Replacing terms:

`b_(yx)=\frac{1050-(13\cdot599)/(7)}{34^{}-((13)^2)/(7)}`

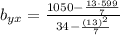
Computing terms:

`b_(yx)=\frac{1050-(7787)/(7)}{34^{}-(169)/(7)}`

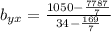
Subtracting terms:

`b_(yx)=\frac{1050-(7787)/(7)}{34^{}-(169)/(7)}=-19/3`

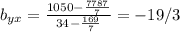
The regression of y on x is as follows:

`y-\bar{y}=b_(yx)(x-\bar{x})`
`y-(599)/(7)=-(19)/(3)(x-(13)/(7))`

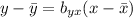
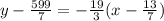
Applying the distributive property:

`y-(599)/(7)=-(19)/(3)x+(247)/(21)`

Now, adding +599/7 to both sides:

`y=-(19)/(3)x+(247)/(21)+(599)/(7)`

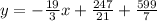
Adding numbers:

`y=-(19)/(3)x+(292)/(3)`

Plugging in x=1.5 into the equation:

`y=-(19)/(3)(1.5)+(292)/(3)`

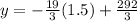
Multiplying numbers:

`y=-9.5+97.3`

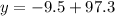
Subtracting numbers:

`y=87.800`

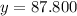
Hence, the solution is as follows:

y_estimated = 87.800