EXPLANATION
Given that we have the data set, we can apply the following representation:
x=0,0.5,1.5,2,2.5,3,3.5
y=96,95,88,85,84,76,75
Building the following table:
Then we have:
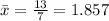
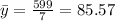
Now,
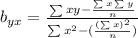
Replacing terms:
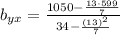
Computing terms:
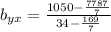
Subtracting terms:
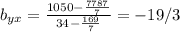
The regression of y on x is as follows:
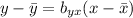
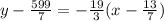
Applying the distributive property:

Now, adding +599/7 to both sides:
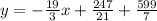
Adding numbers:
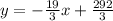
Plugging in x=1.5 into the equation:
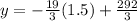
Multiplying numbers:
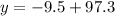
Subtracting numbers:
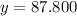
Hence, the solution is as follows:
y_estimated = 87.800