The equation is

.
First, from the rule
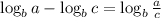
, we rewrite the left hand side as:
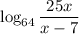
.
Now we write the right hand side as a log with base 64, so that we can make the arguments equal, setting a new equation.
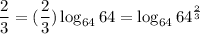
.
We can simplify the argument of this expression into a more manageable expression using the laws of exponents:
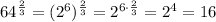
.
Thus, from
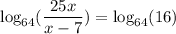
we clearly have:
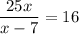
.
For x different from 7:
25x=16(x-7)
25x=16x-112
9x=-112
x=-112/9.
This value is approximately -12.44, so x-7, the argument of both the first and the second expression, would be negative. Thus, the equation has no solution.