SOLUTION:
Case: Inflexion points
A point of inflection is found where the graph (or image) of a function changes concavity. To find this algebraically, we want to find where the second derivative of the function changes sign, from negative to positive, or vice-versa. So, we find the second derivative of the given function.
Given:
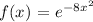
Required:
a) Find the number of critical points
b) Find the x-coordinates of the critical points
Method:
Steps1:
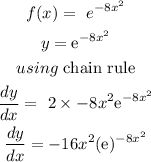
We find the second derivative
![\begin{gathered} (dy)/(dx)=-16x^2\text{e}^(-8x^2) \\ (d^2y)/(dx^2)=256x^2\text{e}^(-8x^2)\text{ - 16}e^(-8x^2) \\ (d^(2)y)/(dx^(2))=\text{ 16}e^(-8x^2)\left(16x^2-1\right? \\ At\text{ critical points, the second derivative equals zero} \\ \text{16}e^(-8x^2)\left(16x^2-1\right?=\text{ 0} \\ \text{16}e^(-8x^2)\text{= 0 OR 16x}^2-1=0 \\ x\text{ is undefined OR 16x}^2=\text{ 1} \\ x^2=(1)/(16) \\ x=\text{ }\sqrt{(1)/(16)} \\ x=\text{ +}(1)/(4)\text{ or -}(1)/(4) \end{gathered}]()
Final answer:
a) The function has 2 inflexion points
b) the values of x are -1/4 and +1/4