Question

“Identify the height of the parallelogram” Would the height be 7 Inches? It’s just what i got, but i want to make sure it’s right. if it’s not right, i need help then

Answer 1

Given the parallelogram below:

According to the properties of a parallelogram, the opposite sides are parallel and equal in dimensions.

Thus,

`\begin{gathered} AD=BC \\ and \\ AB=DC \end{gathered}`

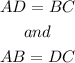
A) Height of the parallelogram:

The length BE is the height of the parallelogram, which is evaluated using the Pythagorean theorem.

According to the Pythagorean theorem,

`\begin{gathered} (BC)^2=(BE)^2+(EC)^2 \\ \end{gathered}`

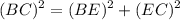
Where

`\begin{gathered} BC=9 \\ BE=h \\ EC\text{ is unknown} \end{gathered}`

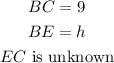
To evaluate h, we need to determine the value of EC.

Recall that

`\begin{gathered} AB=DC \\ where \\ DC=DE+EC \\ \Rightarrow AB=DE+EC \end{gathered}`

Thus, we have

`\begin{gathered} 9=6+EC \\ subtract\text{ 6 from both sides of the equation} \\ 9-6=6-6+EC \\ \Rightarrow EC=3\text{ in.} \end{gathered}`

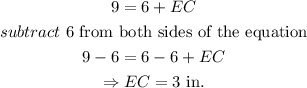
We can now determine the value of h.

From the Pythagorean theorem,