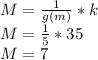Question

Suppose g(m) varies inversely with M and g(m)=3.5 when m=10. what is the value of M when g(m)=5?

Answer 1

In an inverse variation, the function takes the form xy=k
where k is a constant.
Given g(10)=3.5, we find k=xy=3.5*10=35.
This means the function is
m*g(m)=35
When g(m)=5, then m=35/5=7.

Answer 2

M = 7

Explanation:

As g(m) varies inversely with M, that is represented by the expression:

`g(m)=(1)/(M)`

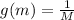
Now we have to introduce a constant of proportionality (k), that is multiplying the function:

`g(m)=(1)/(M)*k`

Then we can replace the given values to find the value of k:

When m=10, g(m)=3.5

`g(m)=(1)/(M)*k\\k=g(m)*M`

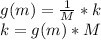
k=3.5*10

k=35

Now, we can replace the given value of g(m)=5 to find M:

`M=(1)/(g(m))*k\\M=(1)/(5)*35\\M=7`