Question

Solve for x. The vertex on the right is labelled as R.

Answer 1

Notice that the marks over the segments QT and TR tell us that those segments are congruent.

Since QT+TR=QR and QT=TR, then QT+TR=QT+QT=2QT.

Therefore:

`QR=2QT`

For a similar argument, we can conclude that:

`QP=2\cdot QS`

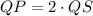
Notice that the segments ST and PR are parallel, because the triangles QST and QPR are similar (this can be demonstrated by the SAS criterion, since QR/QT=QP/QS and both triangles share tha angle Q).

Since ST and PR are parallel, then the angles QST and QPR are corresponding angles and they have the same measure. Furthermore, the angles QST and PST are supplementary angles. Therefore:

`m\angle QST+m\angle PST=180\~`

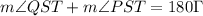
Since the measure of QST is the same as the measure of QPR, which is 5x-9, and the measure of the angle PST is 11x-3, then susbtitute those expressions into the equation:

`(5x-9)+(11x-3)=180`

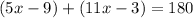
Solve for x:

`\begin{gathered} \Rightarrow5x-9+11x-3=180 \\ \Rightarrow16x-12=180 \\ \Rightarrow16x=180+12=192 \\ \Rightarrow x=(192)/(16) \\ \Rightarrow x=12 \end{gathered}`

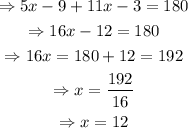
Therefore, x=12.