Question

How to prove that (R,*) is an abelian group.

Answer 1

You need to firstly show that
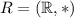
`R=(\mathbb R,*)` is a group, which requires that
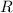
`R` is closed under
`*`, that
`*` is associative,, that
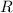
`R` has an identity element, and that every element in
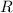
`R` has a corresponding inverse in
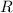
`R`. Then for
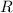
`R` to be abelian, you also need to show that
`*` is commutative.

But suppose
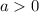
`a>0` and
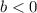
`b<0`, where
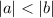
`|a|<|b|`. For instance, take
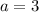
`a=3` and
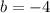
`b=-4`. Then


`3*(-4)=√(3^3+(-4)^3)=√(27-64)=√(-37)\\ot\in\mathbb R`

which means
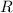
`R` is not closed under
`*` and is therefore not a group, and certainly not an abelian one.