Question

What are the amplitude, period, and midline of f(x)=-4 cos (2x-n)+3?

Answer 1

To find the amplitude and period you need to be familiar with the following equation. Also you need to know that the standard cos has a period of
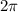
`2\pi` and the midline is a line that runs between the max and min of the y-values of the function.

Equations:
f(x) = A cos(Bx +C) + D
f(x) = -4 cos(2x -n) + 3

A = amplitude = |-4| = 4
B = 2
C = phase shift = n = 0
D = vertical shift = midline = 3

Amplitude = 4

Find the period:

`Period = (2\pi)/(B) = (2\pi)/(2) = \pi`

Find the midline:
We know that the amplitude is 4 so we have a range from -4 to 4. The standard y = cos(x) has its midline at 0 so y = 0. This is also true for y = -4 cos(x). In your equation though, you have a vertical shift of +3 so this changes our midline. With an amplitude of 4, which gives us a range from -4 to 4(our y-values), the shift moves this up by 3 so that means we will have new y-values and a range of -1 to 7. Now we need to find the midline(the middle of our y-values) of our new range. We can find this by using the following formula

`Midline = (Y_1 + Y_2)/(2) = (-1+ 7)/(2) = (6)/(2) = 3`

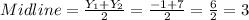Midline:
y = 3

Note, in the following equations that D = 3 = midline

y = A (Bx+C) + D
y = -4 (2x + n) + 3

Also, the picture that is attached is what your equation looks like when graphed.