Question

Which of the following points is not collinear with (3, 6) and (-2, -9)?

A: (-1, -6)
B: (0, -4)
C:(3, 6)
D:(0, -3)

Answer 1

Its B, cause it’s collinear

Answer 2

B: (0, -4)

Explanation:

Three points are collinear if they lie on a single straight line. As we know two points of the line, there is a unique line that passes through both of them.

Let's find the equation of the line:

The general equation of a line is y = mx + b, where m represents the slope and b is the y-intercept.

In this case, we know that

`\left \{ {{6 = m*3 + b} \atop {-9 = m*(-2) + b}} \right. \\`

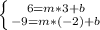
because we want the line to passes through (3, 6) and (-2, -9)

From the first equation, we deduce that
`b = 6 - m*3`

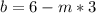
We replace this in the second one and we get

`-9 = (-2)*m + 6 - 3*m\\ -15 = (-5)*m`

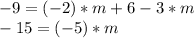
3 = m

With this, b = 6 - 3*m = 6 - 3*3 = -3

b = -3

So, the equation of the line that passes through (3, 6) and (-2, -9) is

`\fbox {y = 3x - 3}`

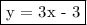
Knowing these, let's see which one of A, B, C or D makes the equation false, i.e. doesn't lie on the line and therefore is not collinear with (3, 6) and (-2, -9). For that, in each case, we have to replace the x of the equation with the first number of the pair and see if it equals the second one.

A: 3*(-1) - 3 = -3 -3 = -6. Correct!

B: 3*0 - 3 = 0 - 3 = -3. Wrong!

C: 3*3 - 3 = 9 - 3 = 6. Correct!

D: 3*0 - 3 = 0 - 3 = -3. Correct!

Therefore, B is not collinear with (3, 6) and (-2, -9)