Question

Which is the polynomial function of lowest degree with rational real coefficients, a leading coefficient of 3 and roots 5 and 2?

Answer 1

A root of a polynomial doesn't mean it is a square root of!!!!!!

P(x)=3(x-5)(x-2)=3x²-21x+30

f (x)= 3 x power point 2 - 21 x + 30

Answer 2

the polynomial is:
`3x^2-21x+30`

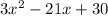
Explanation:

we know that the polynomial function p(x) of lowest degree with roots as 'a' and 'b' and leading coefficient as 'c' is given by:
`p(x)=c(x-a)(x-b)`

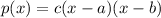
here we are given that the roots are 5 and 2 and the leading coefficient is 3.

so the polynomial p(x) of lowest degree with the above properties is:
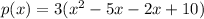
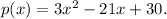`p(x)=3(x-5)(x-2)`

`p(x)=3(x^2-5x-2x+10)`

`p(x)=3(x^2-7x+10)`

`p(x)=3x^2-21x+30.`.