Are exponential growth function.becauese growth factor is greater than one
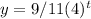

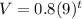
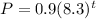
So function:
 and
and
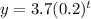 are exponential decaying function.
are exponential decaying function.
Mathematical concepts known as exponential growth and decay are used to explain how a quantity's value changes over time.
A quantity experiences exponential growth when its value rises by a predetermined percentage over a predetermined amount of time.
Conversely, exponential decay happens when a quantity's value drops by a predetermined percentage over a predetermined amount of time.
An exponential growth function often takes the following form:
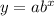
where y is the quantity's value at time x,
an is the quantity's starting value,
B is the factor of growth.
The quantity's value is increasing with time, as indicated by the growth factor being greater than 1.
An exponential decay function generally takes the following form:
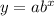
where
a denotes the quantity's initial value and y is its value at time x.
The factor of decay is b.
The quantity's value is decreasing over time, as shown by the decay factor, which ranges from 0 to 1.
Given function;

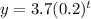
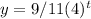

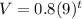
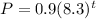
g(x)=2.1(x) is a linear equation and is not an exponential growth or decay function.
For Exponential growth function:The growth factor is greater than 1, indicating that the value of the quantity is increasing over time.
So, function:
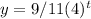

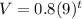
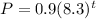
Functions of exponential growth. since the growth factor exceeds one
For the function of exponential decay:
The quantity's value is decreasing over time, as shown by the decay factor, which ranges from 0 to 1.
So function:
 and
and
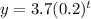 are exponential decaying function.
are exponential decaying function.