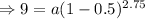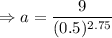Question

A toxic radioactive substance with a density of 9 milligrams per square centimeter is detected in the ventilating ducts of a nuclear processing building that was used 55 years ago. If the​ half- life of the substance is 20 ​years, what was the density of the substance when it was deposited 55 years​ ago?

Answer 1

The density of the substance when it was deposited 55 years​ ago was 60.54 mg/cm³

Explanation:

The exponential function for growth and decay is,

`y(t)=a(1\pm r)^t`

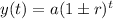
where,

y(t) = the amount after time t

a = initial amount

r = rate of change

t = time period

+ is used for growth and - is used for decay.

As this is the case of decay, so the function becomes,

`y(t)=a(1- r)^t`

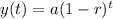
Given,

y(55) = 9 mg/cm³

r = 50% = 0.5 (as the substance is getting halved)

t =
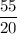`(55)/(20)` = 2.75 (as the half life is 20 years and we have convert time in terms of half life)

Putting the values,

`\Rightarrow 9=a(1- 0.5)^(2.75)`

`\Rightarrow 9=a(0.5)^(2.75)`

`\Rightarrow a=(9)/((0.5)^(2.75))`

`\Rightarrow a=60.54\ mg/cm^3`

Answer 2

60.5 milligrams per square centimeter First, determine how many half lives have expired by dividing the time by the half-life. So: 55/20 = 2.75 That means that only 2^(-2.75) = 0.148650889 = 14.8650889% of the original substance remains. So just divide the amount remaining by 0.148650889 to get the original amount. 9 / 0.148650889 = 60.5445419 So originally, there was 60.5 milligrams per square centimeter 55 years ago.