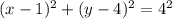Question

What is the standard form of the equation of the circle x2 - 2x + y2 - 8y + 1 = 0

Answer 1

The standard equation of a circle is
`\displaystyle{ (x-a)^2+(y-b)^2=r^2`,

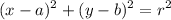
where (a, b) is the center of the circle, and r is the radius.


So, if we write
`x^2 - 2x + y^2 - 8y + 1 = 0` in the above form, the center and the radius will be obvious to us.


Note that
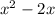
`x^2-2x` is very close to
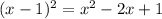
`(x-1)^2=x^2-2x+1` except for the 1.

Similarly, we notice that
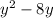
`y^2-8y` is like
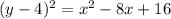
`(y-4)^2=x^2-8x+16`, without the 16.


So,


`x^2 - 2x + y^2 - 8y + 1 = 0\\\\(x^2 - 2x) + (y^2 - 8y) + 1 = 0\\\\(x^2 - 2x+1)-1 + (y^2 - 8y+16)-16 + 1 = 0\\\\(x-1)^2+(y-4)^2-16=0\\\\(x-1)^2+(y-4)^2=16=4^2`.

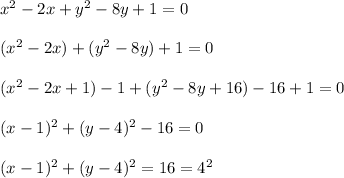
Answer:


`(x-1)^2+(y-4)^2=4^2`