Question

The perimeter of a rectangle is represented by 4x2 + 5x − 2. The perimeter of a smaller rectangle is represented by x2 + 3x + 5. Which polynomial expression BEST represents how much larger the first rectangle is than the smaller rectangle?

Answer 1

A)
`3x^(2) +2x-7`

Explanation:

You need to subtract the perimeter of the smaller rectangle from the perimeter of the larger rectangle.

`(4x^(2) +5x-2) - (x^(2) + 3x +5)`

Distribute -1 (-) to each
`(x^(2) + 3x +5)` :

`4x^(2) +5x-2-x^(2) -3x-5`

Add like terms & solve:

`3x^(2) +2x-7`

Answer 2

`3x^(2) +2x-7`

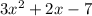
Explanation:

Given :

Perimeter of a bigger rectangle is represented by
`4x^(2) +5x-2`

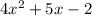
Perimeter of a smaller rectangle is represented by
`x^(2) +3x+5`

To Find : Polynomial expression that represents how much larger the first rectangle is than the smaller rectangle.

Solution :

Subtract the equation of perimeter of smaller rectangle from equation of perimeter of a bigger rectangle :

⇒
`4x^(2) +5x-2 - (x^(2) +3x+5)`

⇒
`4x^(2) +5x-2-x^(2) -3x-5`

⇒
`3x^(2) +2x-7`

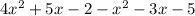
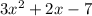
So, Polynomial expression that represents how much larger the first rectangle is than the smaller rectangle is
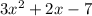`3x^(2) +2x-7`.