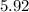Question

C) At the end of the day, the records show that 140 customers made a purchase at the store that day.

What are the mean and standard deviation of the number of customers who won a discount of at
least 30%?

Answer 1

The right solution is "5.92". A further solution is provided below.

Step-by-step explanation:

The given values are:

Total number of customer,

n = 140

The probability of 30% discount,

=
`(1)/(2)`

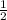
Somewhat by binomial distribution we could perhaps calculate the mean as well as the mean of the standard deviation will be:

=
`140* (1)/(2)`

=
`70`

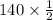
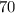
Now,

The standard deviation will be:

=
`√(np(1-p))`

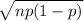
On substituting the given values, we get

=
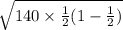
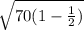
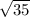
`\sqrt{140* (1)/(2)(1-(1)/(2) ) }`

=
`\sqrt{70(1-(1)/(2) )}`

=
`√(35)`

=
`5.92`