The first step is to write the system of equations as an augmented matrix:
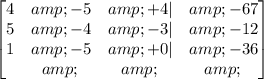
The next step is to let the first number at the mid-row to zero, then let
R2-5/4*R1->R2
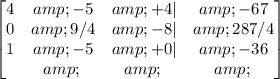
Now, let's convert the first number in the last row to 0, then:
R3-1/4*R1->R3
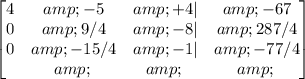
Let's convert the first number in the first row to 1, then:
1/4*R1->R1
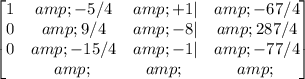
Now, let's convert the second number in the last row to zero:
R3-(-5/3)R2->R3
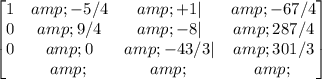
Now let's convert the third number in the last row to 1:
(-3/43)R3->R3
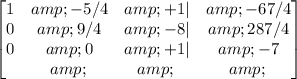
And finally, convert the second number in the mid-row to 1:
(4/9)*R2->R2
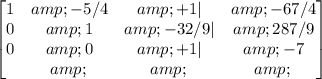
Now, we obtained the next equations:
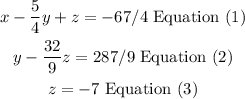
Replace equation 3 into equation 2 and solve for y:
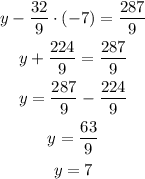
Now, replace x and y in equation 1 and solve for x:
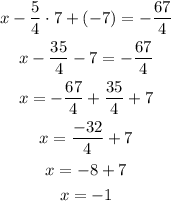
Therefore, the solution set is: (-1, 7, -7)